Liebe Leser,
seien Sie bitte nicht enttäuscht, wenn Sie hier keinen perfekten Text vorfinden. Denn leider bin ich nicht im Besitz eines Nürnberger Trichters. Ich stehe dem Problem gegenüber, es mit Lesern unterschiedlichen Kenntnisstandes zu tun zu haben. Was dem einen zu ausführlich ist, findet der andere zu knapp. Ich habe mich deshalb zu dem Versuch entschlossen, mit einer knappen Version zu beginnen. Sie, die Leser, können mir per E-Mail
bruhn@mathematik.tu-darmstadt.de
mitteilen, wo Sie Probleme haben. Ich werde mich dann durch Abändern oder Erweitern des Textes um Abhilfe bemühen.
Meylsche Skalarwellen - ganz einfach
Gerhard W. Bruhn, Technische Universität Darmstadt
Übersicht K. Meyl hat seine Skalarwellen als Vektor-Lösungen seiner Fundamentalen Feldgleichung (FFG) definiert, die ein skalares Potential besitzen (Skalarwellenbedingung (S)). Naturgemäß bewegen sich Wellen von der Stelle, und das hat Meyl auch verschiedentlich in Abbildungen dokumentiert. Er hat jedoch übersehen, dass man die allgemeine Lösung von (FFG) und (S) leicht bestimmen kann. Es zeigt sich, dass alle möglichen Lösungen ortsfest sind. Bewegliche, d.h. Meylsche Skalarwellen, kann es nicht geben. Das gleiche gilt auch für Meyls Plasmawellen, sogar ohne Berufung auf (S).
Basis ist K. Meyls Fundamentale Feldgleichung (FFG) in der Fassung seines Buches EMV 3 von 2003, S.118, s. Anhang. Nach vereinfachter Benennung der Koeffizienten haben wir damit die partielle Differentialgleichung
(FFG) − c2 rot rot E = Ett +(α+β) Et + αβ E (mit α,β konstant ≥ 0, c = Lichtgeschw.).
als Ausgangspunkt.
Eine Skalarwelle ist dann eine Lösung E(x,t) der FFG, die ein skalares Potential U(x,t) besitzt, d.h. sich in der Form
(P) E = (E1, E2, E3) = grad U = (∂U/∂x1, ∂U/∂x2, ∂U/∂x3)
durch Differentiation aus dem Potential U gewinnen lässt. Aber, das Problem ist, dass man bei einem gegebenen Feld E nicht ohne weiteres sehen kann, ob ein passendes Potential existiert, und welches. Aber es gibt ein einfaches Kriterium für die Existenz eines Potentials zu E, die Bedingung
(S) rot E = (∂E3/∂x2− ∂E2/∂x3, ∂E1/∂x3− ∂E3/∂x1, ∂E2/∂x1− ∂E1/∂x2) = 0,
die wir als Skalarwellenbedingung bezeichnen wollen (S.6 in Meyls Buch EMV 3).
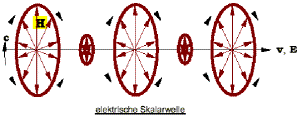
Nach Meyl sind Skalarwellen Lösungen der Gleichungen (FFG) und (S), die sich mit einer Geschwindigkeit v ≠ 0 durch den Raum bewegen, s. die Abbildung aus Meyls Buch S.22
Wir wollen jetzt - über Meyl hinausgehend - die allgemeine Lösung der Gleichungen (FFG) und (S) bestimmen und anschließend deren Fortbewegungseigenschaft diskutieren.
Wegen rot 0 = 0 erhalten wir bei Einsetzen von (S) in (FFG)
Ett + (α+β) Et + αβ E = − c2 rot 0 = 0.
Der Erfolg des Einsetzens ist, dass keine Ortsableitungen mehr vorkommen, wir haben eine Differentialgleichung erhalten, die nur noch E und Zeitableitungen davon enthält: Aus der partiellen Differentialgleichung (FFG) ist die (bzgl. der Zeit t) gewöhnliche Differentialgleichung
(1) Ett +(α+β) Et + αβ E = 0
geworden.
Meyl betrachtet auch sog. Plasmawellen, d.h. Wellen der Ladungsdichte ρ = ε div E . Hierzu gibt es wegen der Quellenfreiheit aller Wirbelfelder, also wegen der Identität div rot = 0 , eine einfache Folgerung aus Meyls (FFG), die sogar ohne die Verwendung der Skalarwellenbedingung (S) auskommt: Die Bildung der Divergenz der (FFG) liefert nach Multiplikation mit dem konstanten Faktor ε
(1') ρtt +(α+β) ρt + αβ ρ = 0
Das Fehlen der Ortsableitungen in (1) und (1') gestattet bereits ohne explizite Kenntnis der Lösungen eine wichtige Folgerung: Die (FFG) (für E mit (S)) bestimmt nur die zeitliche Änderung von Feldstärke E bzw. Ladungsdichte ρ bei festem Ort x:
Eine Zustandsbeeinflussung von Ort zu Ort, eine Wellenfortpflanzung, findet nicht statt.
Damit sind die sich mit v ≠ 0 durch den Raum bewegenden "Skalarwellen" von Meyls Abbildung nicht möglich.
Diese für Meyls Skalarwellen fatale Ortsfestigkeit von E und ρ wird im folgenden noch deutlicher werden. (1) (analog (1')) ist eine gewöhnliche lineare Differentialgleichung zweiter Ordnung mit konstanten Koeffizienten. Für Gleichungen dieses Typs werden durch den Exponentialansatz E = E0 eλt mit konstantem Vektor E0 ein passendes λ bestimmt. Durch Einsetzen des Ansatzes in die Differentialgleichung (1) kommt man auf die sog. charakteristische Gleichung
(2) λ2 + (α+β) λ + αβ = 0,
eine quadratische Gleichung für λ, deren Lösungen λ1= − α und λ2= − β man erraten (und natürlich auch ausrechnen) kann. Die Theorie der gewöhnlichen Differentialgleichungen lehrt, dass man aus den speziellen Ansatzlösungen
E1 e−αt und E2 e−βt mit E1, E2 konstant
die allgemeine Lösung von (2) im Fall α ≠ β (der Spezialfall α = β wird hier weggelassen.)
E1 e−αt + E2 e−βt
zusammensetzen kann. Die Konstanz von E1 und E2 bezieht sich nur auf die Zeit t. Beide dürfen von der Ortsvariablen x abhängen, ohne das Bestehen der t-Differentialgleichung (1) zu beeinträchtigen. Ausgeschrieben kennen wir also die allgemeine Lösung von (1), sie lautet:
(3) E(x,t) = E1(x) e−αt + E2(x) e−βt
Aber die Skalarwellenbedingung ist durch (3) noch nicht erfüllt. Doch genügt es dazu nach (P), die Koeffizienten E1 und E2 aus Potentialen U1(x) und U2(x) zu gewinnen. Dann hat man mit
(4) E(x,t) = e−αt grad U1(x) + e−βt grad U2(x).
die allgemeine Lösung des Meylschen Problems (FFG) & (S) für den Fall α ≠ β gefunden, wobei die Potentialfunktionen U1(x) und U2(x) willkürlich gewählt werden dürfen.
Unter diesen Darstellungen aller Lösungen müssen sich (wenn existent) die Meylschen Skalarwellen befinden.
Angenommen, eine "Skalarwelle" befinde sich für t=0, von einem Sender erzeugt, im Innern einer Kugel K. Im "Außenraum" außerhalb von K ist dann als Anfangszustand für t = 0 Feldfreiheit E = 0 und Et = 0 anzunehmen. Diese Anfangsbedingung hat
grad U1(x) ≡ 0 und grad U2(x) ≡ 0 außerhalb von K
und dann nach (4) auch E ≡ 0 im Außenraum für alle t zur Folge: Die in K erzeugte "Skalarwelle" wird K nie verlassen und kann deshalb nicht in den Außenraum eindringen. Diese ortsfeste "Welle" ist mit Sicherheit keine Skalarwelle i.S. von K. Meyl, der sich bei vielen Gelegenheiten festgelegt hat (s. z.B. die oben gezeigte Abbildung):
Eine Skalarwelle bewegt sich nach K. Meyl mit einer Geschwindigkeit v≠ 0 durch den Raum. Doch das Meylsche Problem (FFG) & (S) besitzt keine derartigen Lösungen, m.a.W.:
Es gibt keine Meylschen Skalarwellen.
Literatur
K. Meyl: Elektromagnetische Umweltverträglichkeit Teil 3, Indel-Verlag 2003
http://www2.mathematik.tu-darmstadt.de/~bruhn/DGEIM-Tagung_2003.doc
http://www2.mathematik.tu-darmstadt.de/~bruhn/DGEIM-Tagung_2003.htm
Anhang
Meyls Herleitung der Fundamentalen Feldgleichung aus EMV 3, S.118