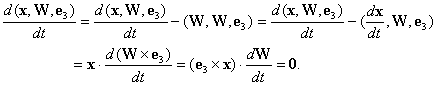Zur Kontraktion des reibungsfreien Achsialwirbels

Von G.W. Bruhn, Technische Universität Darmstadt

Im folgenden wird die Kontraktion eines reibungsfreien Achsialwirbels um die vertikale e₃-Achse behandelt, indem mit Hilfe von Erhaltungssätzen Aussagen über die Änderung der beteiligten Zustandsgrößen gemacht werden.

1. Bezeichnungen

Ortsvektor des R³ x Druck p

Zeit t Massendichte r

Schwerkraft rg = –rge₃ Schwerebeschleunigung g

Temperatur T

Spez. Energie e = c_vT Spez. Enthalpie i = c_pT

Vektor der Strömungsgeschwindigkeit ,

zerlegt bezüglich Zylinderkoordinaten (r, J, z) um die vertikale e₃-Achse. n ist der radiale Einheitsvektor ^ e₃ und t = e₃ × n der azimutale Einheitsvektor (tangential zu den koaxialen Zylinderflächen um die z-Achse).

Substantielle Ableitung

Jede Lösung x(t) der Differentialgleichung

heißt Substanzlinie. Die substantielle Ableitung differenziert nach der Zeit entlang der Substanzlinien x(t), d.h. es gilt die "Kettenregel"

.

2. Die allgemeinen Grundgleichungen

Kontinuitätsgleichung (1) ,

Euler-Gleichung (2) ,

Energiegleichung (3a) .

Thermo-Energiesatz (3b) mit

Thermodynamische Beziehungen für ideale Gase konstanter spez. Wärmen c_p und c_v.

3. Erhaltungsgrößen

Folgerung 1. Bei allen reibungsfreien Strömungen bleibt die (spezifische) Entropie s längs der einzelnen Substanzlinien konstant, d.h. die Entropie s ist eine Erhaltungsgröße.

Folgerung 2. Kommen alle Substanzlinien aus einem Bereich mit einem einheitlichen Wert s₀ der Entropie, so gilt s = s₀ global in der ganzen Strömung, die Strömung ist isentropisch.

In einer isentropischen Strömung gilt global , die Strömung ist mithin auch barotrop, . Für barotrope Strömungen gilt somit auch . Daher liefert die Anwendung des rot-Operators auf die Eulersche Gleichung in der Form

die Beziehung , oder mit

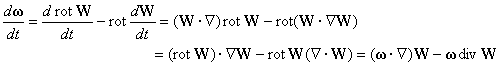
Folgerung 3. Bei barotropen Strömungen bleibt längs Substanzlinien erhalten. Kommen alle Substanzlinien einer barotropen Strömung aus einem wirbelfreien Bereich, so ist die Strömung insgesamt wirbelfrei. Dies gilt insbesondere für isentropische Strömungen.

Wir betrachten speziell achsialsymmetrische Strömungen um die vertikale Richtung e₃ || g.

Bei Achsialsymmetrie um e₃ gilt . Daher erhält man aus

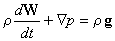| × (x × e₃)

die Beziehung

Folgerung 4. Für reibungsfreie achsialsymmetrische Strömungen um die Vertikale ist auch der Drehimpuls eine Erhaltungsgröße.

Für stationäre Strömungen gilt . Daher ergibt sich bei Reibungsfreiheit aus

die Gleichung , und mit wegen längs der Substanzlinien konstanter Entropie folgt .

Folgerung 5. Für reibungsfreie stationäre Strömungen ist auch die Bernoulli-Kombination eine Erhaltungsgröße.

Für z-unabhängige achsialsymmetrische (s. den folgenden Abschnitt) stationäre Strömungen nimmt die Kontinuitätsgleichung die Form

an. Damit haben wir

Folgerung 6. Für z-unabhängige achsialsymmetrische stationäre Strömungen ist eine weitere Erhaltungsgröße.

4. Achsialsymmetrische Strömungen

Ortsvektor im R³

Azimutalvektor

Geschwindigkeitsvektor

Radialanteil von W ,

Azimutalanteil von W

Vertikalanteil von W

Divergenz von W

nach Bronstein, 18. Aufl., S.466 und wegen Rotationssymmetrie.

Damit nehmen die Grundgleichungen die folgende Form an:

Kontinuitätsgleichung .

Im stationären Fall erhält man daraus

oder

.

Außerdem ist die vertikale Euler-Gl. zu erfüllen:

Hinzu kommen die Erhaltungsgrößen s, rv und im stationären Fall auch .

5. Der Zustandsverlauf längs einer Stromlinie

Betrachtet wird ein stationärer Wirbel, der aus kreisförmigen Stromfäden um die Wirbelachse, die z-Achse, besteht. Dieses System von Stromfäden möge nun mit kleiner Radialgeschwindigkeit u kontrahieren. Dadurch werden aus den ursprünglichen geschlossenen Kreisbahnen Spiralen, aber immer noch bleiben die zu irgendeiner Zeit auf einem zur z-Achse konzentrischen (zur Achse senkrechten) Kreis befindlichen Massenteilchen weiterhin auf einem solchen Kreis, der allerdings einen schrumpfenden Radius besitzt.

Es wird angenommen, dass der Kontraktionsprozess wiederum stationär erfolgen soll, also mit der radialen Kontraktionsgeschwindigkeit u=u(r,z). Dann stehen längs jeder Stromlinie die drei ersten genannten Erhaltungsgrößen zur Verfügung.

Es wird der Wirbel im Bereich oberhalb des Bodens, also für z > 0, betrachtet. Die Erhaltungsgröße rv führt mit einer stromlinien-abhängigen Konstanten c zu:

rv = c.

Die Bernoulli-Erhaltungsgröße liefert dann

d.h. für eine Stromlinie durch (r₀,z₀) mit dem Zustand (W₀, T₀) erhält man

.

Weil die linke Seite bei Annäherung an die Wirbelachse, für r ® 0, stark wächst, muss dies auch der Term T₀- T tun.:

Folgerung. Die Temperatur auf einem kreisförmigen zur Achse konzentrischen Massenbereich muss bei Kontraktion, bei Annäherung an das Wirbelzentrum, stark fallen, unabhängig von der sonstigen Form der Stromlinien. Auch das Ausweichen der Strömung in vertikaler Richtung (s.u.), d.h. wachsendes z, verursacht durch den negativen Term z₀- z zusätzliche Abkühlung.

Auch über das Verhalten der Vertikalgeschwindigkeit w bei Annäherung an die Achse lässt sich leicht eine Aussage machen. Wir betrachten dazu in einen zur Wirbelachse koachsialen Zylinder vom Radius R und der Höhe H über der Grundebene z = 0. Durch die Grundfläche findet (nach Annahme) kein Massentransport statt. Auf der Zylindermantelfläche ist wegen Kontraktion die radiale Geschwindigkeit <0, d.h. hier strömt Materie in den Zylinder ein. Wegen Massenerhaltung muss diese Materie durch die obere Deckelfläche (für z = H) wieder ausströmen. Daher gilt:

Wenn die Radialgeschwindigkeit auf dem Zylindermantel (im Massen-Mittel) < 0 ist, so muss die Vertikalgeschwindigkeit w auf der Deckel-Kreisfläche (im Massen-Mittel) > 0 sein. Diese Überlegung lässt sich mit Hilfe des Gaußschen Satzes unter Verwendung der Kontinuitätsgleichung aus Abschnitt 4 auch exakt begründen.