Zur Rolle des magnetischen Vektorpotentials beim
Aharonov-Bohm-Effekt
Gerhard W. Bruhn, Fachbereich Mathematik der TU Darmstadt
Betrachtet wird der bekannte Versuch der Beugung von Elektronen an einem Doppelspalt, wobei auf einem Bildschirm hinter der Doppelspalt-Blende ein Interferenzmuster der Häufigkeit auftreffender Elektronen entsteht.
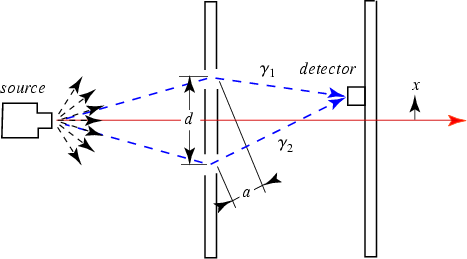
Beim Aharonov-Bohm-Versuch wird nun im Bereich zwischen den beiden Schlitzen zusätzlich senkrecht zur Zeichenebene ein Magnetfluss B mit dem Vektorpotential A eingeschaltet.
(1) B
= rot A.
Man kann den Fluss sogar so eingrenzen, dass in dem für Elektronen zugänglichen Bereichen kein Fluss stattfindet, dort also B = 0 gilt. Dennoch "fühlen" die Elektronen das Magnetfeld, es kommt zu einer Verschiebung des Interferenzmusters.
Die Phasendifferenz der auf dem Bildschirm auftreffenden Wahrscheinlichkeitswellen wird durch dieses Magnetfeld verändert um
(2) 2π/h q ( ∫γ1 A·dx − ∫γ2 A·dx )
verschoben. Vordergründig gesehen hängt also die Phasenverschiebung von dem Vektorpotential A ab.
Das hat oberflächlich denkende Betrachter zu der Meinung verleitet, hier sei zum ersten Mal in der Physik eine direkte Wirkung eines Vektorpotentials zu erkennen. Doch diese Ansicht ist irrig: Denn die Wegintegrale in (2) lassen sich unter Umkehrung der Durchlaufungsrichtung des Weges γ2 umschreiben in
(3) 2π/h q ∫γ1−γ2 A·dx ,
wobei γ1−γ2 jetzt einen geschlossenen Weg bezeichnet. Aber hier kann der Stokes’sche Integralsatz angewendet werden
∫γ1−γ2 A ·dx = ∫∫Ωrot A · do,
wobei Ω die in den geschlossenen Weg γ1−γ2 eingespannte Fläche bedeutet. Mithin erhält
man statt (3)
(4)
2π/h
q ∫∫Ωrot A · do = ∫∫Ω B · do.
Damit ist ersichtlich die Phasenverschiebung
des Aharonov-Bohm-Effekts allein vom Fluss B des wirksamen Magnetfelds
abhängig. Eine Abhängigkeit von der im Vektorpotential A enthaltenen zusätzlichen
Information - A ist ja nur bis auf einen additiven Gradienten
bestimmt - lässt sich nicht beobachten:
Wirksam
für die Phasenverschiebung ist allein der magnetische Fluss B.
Die Elektronen "fühlen" nur den magnetischen Fluss B, nicht aber die in dessen Vektorpotential A enthaltenen Zusatzinformationen.
Literatur
R.P. Feynman, R. B. Leighton, M. Sands: The Feynman Lectures on Physics, Addison Wesley 1963, mit deutscher Übersetzung im Oldenbourg-Verlag 1973, Teil II-1, S. 15-11 ff.
L. Motta, Aharonov-Bohm Effect, Eric
Weisstein's World of Physics
http://scienceworld.wolfram.com/physics/Aharonov-BohmEffect.html