Der Dissipationsterm in den Navier-Stokes-Gleichungen

Gerhard Bruhn, Technische Universität Darmstadt

g.w.bruhn@t-online.de

W.M. Bauer behauptet in seinem von den Gläubigs dieser Welt hochgeschätzten Buch [1] wiederholt, der Dissipationsterm der Navier-Stokes-Gleichungen könne sich in gewissen Fällen auf die Strömung auch beschleunigend auswirken. Er und seine Anhänger bezeichnen diesen Effekt auch als „Selbstbeschleunigung von Wirbeln“ und leiten aus dem Effekt die sagenumwobene „Entropievernichtung“ in Tornados ab, die in den Augen der „Schulwissenschaft“ schlicht eine Verletzung des 2. Hauptsatzes der Thermodynamik darstellt.

Im folgenden wird gezeigt werden, dass der Dissipationsterm seinen Namen zu Recht trägt und bei Wahl physikalisch sinnvoller Dissipationskoeffizienten immer eine Entropie-vernichtung verhindert. Auf dieser Basis kann keine Widerlegung des 2. Hauptsatzes durchgeführt werden. Bei Gültigkeit der Navier-Stokes-Gleichungen ist die Entropie längs der Substanzlinien eine zeitlich nicht abnehmende Funktion. Dies ist Stand der Wissenschaft seit vielen Jahren vor Bauers Buch [1]. Wenn W.M. Bauer dennoch in [1] zu dem entgegengesetzten Resultat kommt, liegt das allein an seiner Unfähigkeit, etwas kompliziertere Rechnungen fehlerfrei zu Ende zu führen. Außer der Fähigkeit, große Sprüche zu klopfen, stellt W.M. Bauer in [1] auch bei anderen Anlässen seine Unfähigkeit, richtig zu rechnen, großzügig unter Beweis.

Wir beginnen mit den Navier-Stokes-Gleichungen in der Form

wie sie in der Strömungsmechanik üblich sind, s. z.B. K. Wieghardt [2], S.42. Dabei werden die Zähigkeitskoeffizienten als konstant angenommen. Obwohl W.M. Bauer in den Heften 1-4 seines Buches die Gleichungen immer wieder erwähnt, findet sich eine Darstellung der Navier-Stokes-Gleichungen an keiner Stelle des Buches, auch nicht in einem Abschnitt gleichen Namens. Aber – in Heft 4, Abschnitt 3, Entropie in Wirbeln, wird eine „Zusatzbeschleunigung der Navier-Stokesschen Gleichungen“ eingeführt.

lässt sich aus der rechten Seite von (1) durch die Wahl erhalten, so dass die oben geforderte Koeffizientenbedingung gerade noch erfüllt ist.

Um die Dissipationseigenschaft der Zusatzterme in (1) nachzuweisen, benötigen wir zunächst den Energiesatz (s. [2], S.141-142 oder [3], S.60 ff.)

und die skalar mit w multiplizierte Bewegungsgleichung (1)

Subtraktion von (2) ergibt

mit

und

Mit Hilfe der Kontinuitätsgleichung in der Form

,

lässt sich der 1. Hauptsatz zur linken Seite von (2') passend umformen zu

.

Einsetzen von (2') in (3) ergibt

.

Diese Gleichung beschreibt das zeitliche Verhalten der Entropie s. Die Größen und sind positiv. Um nachzuweisen, braucht im Fall nur noch gezeigt zu werden. Dazu schreiben wir bezüglich kartesischer Koordinaten x_k (k =1,2,3) aus und benutzen die sehr praktische Einsteinsche Summationskonvention: Bei Produkten wird über gleichlautende Indizes (ohne Hinschreiben des Summenzeichens) automatisch summiert.

Beispiel. bedeutet . Auf diese Weise lassen sich Skalarprodukte sehr bequem in Koordinaten ausschreiben: .

erhält man mit dem formalen Vektor und die Umschreibung:

.

Man muss beim Umschreiben der Skalarprodukte sehr genau darauf achten, wer mit wem da ein Skalarprodukt bildet. Dann aber kann flott – unter Verwendung der Regeln für partielle Ableitungen, z.B. Produktregel, , usw. – gerechnet werden. Zur Abgrenzung der Wirkungsbereiche der Ableitungen werden Klammern verwendet:

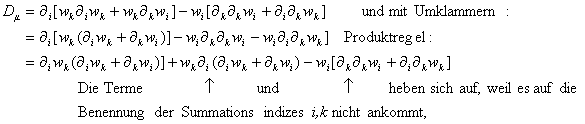
Im allgemeineren Fall erhält man

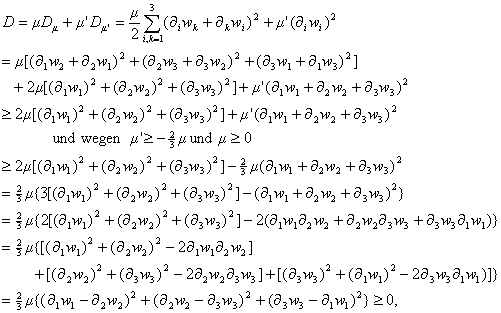
d.h. für Zähigkeitskoeffizienten erhält man nichtnegative Dissipation D. Andererseits liefert die spezielle Strömung den Wert

,

so dass D ³ 0 für bei beliebiger Strömung nicht möglich ist.

Ergebnis.

Die Reibungsterme auf der rechten Seite der Navier-Stokes-Gleichungen (1) verhalten sich genau dann dissipativ, wenn die Zähigkeitskoeffizienten den Bedingungen genügen. Unter diesen Bedingungen kann die Entropie s längs jeder Teilchenbahn (Substanz-Linie) nicht abnehmen. Eine Bauersche „Entropievernichtung“ ist daher bei Gültigkeit der Navier-Stokes-Gleichungen mit den angegebenen Zähigkeitskoeffizienten nicht möglich.

Zusatz. Das Auftreten von Stößen wurde hier nicht behandelt. Mathematisch gestatten die einschlägigen Rankine-Hugoniot-Stoßgleichungen Stöße mit Entropie-Zuwachs wie auch mit Entropie-Abnahme. Aber Stöße mit Entropie-Abnahme sind in der überreichen experimen-tellen Praxis nie beobachtet worden.

Literatur

[1] Wilhelm M. Bauer, Die Welt der Wirbel und Atome Bde. I u. II, DELTA PRO DESIGN VERLAG, Berlin 1997, ISBN 3-980 5355-2-5 und 3-980 5355-3-5

[2] K. Wieghardt, Theoretische Strömungslehre, Teubner 1974

[3] J. H. Spurk, Strömungslehre, 3. Auflage, Springer 1993, ISBN 3-540-55077-1