Ein Vorschlag zur radikalen Vereinfachung des SMOT

von E.S. Gullible, Technische Universität Darmstadt

 

Wenn die sensationellen Nachrichten in [1] über SMOT, das Simple Magnetic Overunity Toy, zutreffen, kann man mit wenig Mathematik – so wird in dem folgenden Beitrag gezeigt – das Gerät ganz wesentlich vereinfachen und damit viel Geld und Mühe sparen: Eine Stahlkugel im Feld eines einzigen Stabmagneten vollbringt die gleiche Leistung, wie das ganze komplizierte SMOT.

 

1.     Die durch Bewegung in einem Kraftfeld F erzielbare Energie

Ein Körper bewege sich unter dem Einfluss des Kraftfeldes F(x) entlang der Bahnkurve C mit der Gleichung x = x(t) vom Anfangspunkt x(a) = a zum Endpunkt x(b) = b. Dann ist die vom Kraftfeld F(x) bei der Bewegung  geleistete Arbeit (= Kraft mal Weg)

Insbesondere erhält man für einen geschlossenen Weg, also für a = b,

Es gibt Kraftfelder, bei denen A0 immer Null ist, z.B. das Schwerefeld G der Erde: Durch Fallenlassen eines Körpers kann man Energie gewinnen. Bringt man den Körper anschließend in seine Ausgangsposition zurück, muss man die gerade gewonnene Energie zum Anheben des Körpers wieder verbrauchen, insgesamt hat der Kreisprozess keinen Energiegewinn gebracht. Allenfalls hat man Reibungsverluste, die hier vernachlässigt werden.

Aber es gibt auch Felder, in denen die Bewegung längs eines geschlossenen Weges einen Energiegewinn abwirft, z.B. wenn F ein Kreiswirbelfeld ist.

Bewegt sich der Körper der Masse m unter dem Einfluss eines Kraftfeldes F(x) von einem Punkt a zu einem Punkt b längs der Verbindungskurve C, so gewinnt er dabei kinetische Energie. Die Bewegungsgleichung lautet

Der Körper ändert seine Geschwindigkeit gemäß (1.4) und damit auch seine kinetische Energie: Multipliziert man (1.1) skalar mit dem Geschwindigkeitsvektor   und integriert über das Zeitintervall [a,b], so erhält man die Änderung der kinetischen Energie in diesem Zeitraum:

D.h. die aus dem Kraftfeld F(x) gewonnene Energie findet sich gerade in der Erhöhung der kinetischen Energie wieder. Aber man kann den Film auch rückwärts ablaufen lassen, dann wird bei Durchlaufung des umgekehrten Weges die kinetische Energie  wieder verbraucht, um die Masse m längs C zurück von b  nach a zu bringen.

 

2.     Zusammengesetzte Kräfte

Häufig, so auch beim SMOT, besteht die wirksame Kraft aus mehreren Anteilen, es ist also

G  sei die Schwerkraft und die Summanden Fk sind die Kraftfelder der insgesamt beteiligten Magnete.

Für das Durchlaufen eines geschlossenen Weges C ergibt Einsetzen in (1.2), dass die Gesamtarbeit A0= A0(F) gleich der Summe der Arbeiten A0(Fk)  und A0(G) ist:

(2.2)    

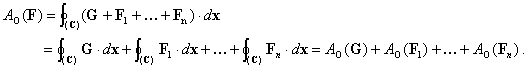
Aber nach Abschnitt 1 wissen wir bereits, dass G keinen Beitrag leistet, A0(G)=0.

Andererseits wird in [1] glaubhaft versichert, dass die bei Durchlaufung einer zyklischen Bahn im SMOT soviel Energie A0(F) anfällt, dass die Reibung überwunden werden kann und die Kugel beliebig lange läuft: „Zumindest sollen solche Geräte schon mehrere Tage gelaufen sein ...“ teilt uns der Autor von [1], Andreas Hecht, mit, und der wird doch wohl keine FOAF-Geschichten weitergeben oder gar FOAFOAF-Geschichten. (FOAF bedeutet “<told by a> Friend Of A Friend“).

Damit können wir sicher sein, dass A0(F) > 0 ist. Aber A0(F) ist die Summe der Summanden A0(Fk). Damit die Summe positiv ausfällt, muss mindestens einer der Summanden A0(Fk) ebenfalls positiv sein. Das bedeutet, dass mindestens einer der Magnete allein schon einen positiven Energiebeitrag liefert, wenn die Kugel die geschlossene Bahn C durchläuft.

Ergebnis. Bereits ein einziger Magnet reicht aus, um qualitativ die gleiche Leistung zu erbringen, wie das ganze SMOT. Man kann sich also zumindest die kostspielige Beschaffung aller übrigen Magnete ersparen, wenn nicht noch mehr ...

Zum Schluss noch eine FOAF-Story: Ein Freund sagte mir, er habe gehört, dass in manchen Büchern der Schulphysik stünde, auch Magnetfelder F hätten wie G die Eigenschaft A0(F)=0 für jeden geschlossenen Weg C. Wenn das wahr wäre und nicht nur eine FOAF-Geschichte, hätte Andreas Hecht uns ein Märchen erzählt. Ich bin jetzt wirklich ganz verunsichert.

 

Quellenangabe

 [1]      Andreas Hecht, Freie Energie – Eine Einführung,

http://www.borderlands.de/energy.intro.php3