Zwölf Fragen an Professor K. Meyl
gestellt von
Gerhard W. Bruhn, Fachbereich Mathematik der TU Darmstadt
Herr Prof. Dr. K. Meyl, bekannter Fachmann für Skalarwellen und
Neutrinos, hat es für angebracht gehalten, im Rahmen einer Diskussion in der
Zeitschrift CO’MED, Heft 01/2003,
über seine Skalarwellen als Antwort auf sachliche Kritik an seinen
Thesen, sozusagen als kleinen Scherz unter Kollegen, die nebenstehende Replik
zu schreiben. Leider aber hat er vergessen, dem höchst interessierten Leser
mitzuteilen, welche "namhaften Universitätsprofessoren der Mathematik" denn
nun seine profunden Rechnungen überprüft haben - und so wird wohl der
"betrügerische Rentner Bruhn" noch geraume Zeit sein Unwesen treiben.
|
K. Meyl in CO’MED
01/2003
|
Anlässlich eines "denkwürdigen" Vortrages des Kollegen Meyl an der FH Furtwangen am 5.6.2002, also vor fast einem Jahr, erlaubt sich besagter Rentner, dem Vortragenden erneut einige Fragen zu stellen. Die Leser von CO’MED wie auch die Teilnehmer des CEE-Diskussionsforums würden es sehr begrüßen, wenn der Angesprochene sich im Forum
http://cee-200.cee.fh-furtwangen.de/cee_forum/viewforum.php?f=1
oder an anderer Stelle zur Sache äußern würde.
Frage 1 zu den Grundgleichungen und der Longitudinalität der Skalarwellen:
Wie vertragen sich Ihre Grundgleichungen der Elektrodynamik aus
http://www.k-meyl.de/Aufsatze/Objektivitatst._1/objektivitatst._1.html
und Ihren weiteren Veröffentlichungen,
(M 3) E = μ v × E
und
(M 4) H
= − ε v × E,
nach denen die
Vektoren E und H beide senkrecht zu v sein müssen, mit den in
http://www.k-meyl.de/Aufsatze/Teslastrahlung.pdf
gezeigten
Abbildungen je einer elektrischen und einer magnetischen Skalarwelle,
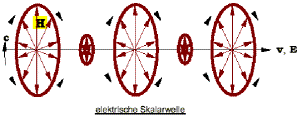
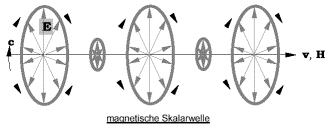
in denen einmal
E parallel zu v und zum anderen H parallel zu v gezeigt wird?
Frage 2 zu Ihren Grundgleichungen (s. Frage 1)
Für beliebiges E0 senkrecht zu v bilden die Vektorfeldpaare (E+,H+) und (E−,H−) mit
(1) E± = E0 eiω(t±x/c)
und
H± = −εv±×E0 eiω(t±x/c)
je eine Lösung Ihrer Grundgleichungen (M 3-4), wenn man v± = ± ce mit dem festen Einheitsvektor e=(1,0,0) wählt. In der Elektrodynamik ist bekannt, dass auch die Überlagerung von zwei Wellen wieder eine mögliche Welle ist: Im vorliegenden Fall ist
(2)
(E++ E−,H++
H−) = 2 (E0, −εv×E0) eiωt cos ωx/c.
eine bekannte Welle, eine sog. "stehende Welle".
Die Frage:
Für welches v ist (2) eine Lösung Ihrer Grundgleichungen?
Oder sollten vielleicht Ihre "Grundgleichungen" (M 3-4) gar keine sein?
Frage 3 zu Ihren Grundgleichungen (s. Frage 1)
Gibt es für |v| ≠c (mit c2=(εμ)−1) nichttriviale Lösungen Ihrer Grundgleichungen (M 3-4)? Wenn ja, erbitten wir ein Beispiel.
Frage 4 zur neuen Großzügigkeit bei Herleitungen
Auf S. 126 Ihres neuen Buches EMV-3 weisen Sie sehr richtig nach, dass Ihre Grundgleichungen (M 3-4 in Frage 1) nur für v = |v| = c, c2 = (εμ)−1, miteinander verträglich sind.
Frage: Weshalb dürfen Sie dann in Ihrer Gleichung (27.27), die ja auf dem gleichen Mist gewachsen ist, dennoch auch die Fälle
v < c und v > c
in Betracht ziehen?
War Ihnen das bei Niederschrift von S. 122 noch nicht bekannt? In Ihrem
war davon jedenfalls noch nicht die Rede.
Frage 5 Kann man Äpfel und Birnen
addieren?
Sie schreiben in EMV-3, S. 89: "Longitudinalwellen kennen bekanntlich keine feste Ausbreitungsgeschwindigkeit. Da sie in Richtung eines schwingenden Feldzeigers laufen, wird auch der Geschwindigkeitsvektor schwingen." Diesen aufregenden Effekt, den wir vorher noch nicht kannten, wollen wir uns an einem Beispiel klarmachen:
Frage: Wie kann sich
denn bei einer elektrischen Skalarwelle die longitudinal schwingende Feldstärke
E, die in der Maßeinheit Volt/Meter gemessen wird, zu der
Ausbreitungsgeschwindigkeit, gemessen in km/sec, addieren? Was gibt z.B. eine
longitudinal um +10 Volt/Meter schwankende Feldstärke, wenn man diese
Schwankung, sagen wir, zur Lichtgeschwindigkeit c = 300000 km/sec addieren
will? Liegt die schwankende Geschwindigkeit nun zwischen 299990 km/sec und
300010 km/sec? Oder muss man die Feldstärke zuvor noch auf Volt/km umrechnen? Dann käme man mit +10000
Volt/km auf die aufregende Geschwindigkeitsschwankung zwischen 290000 km/sec
und 310000 km/sec? Was ist da richtig, Herr Meyl?
Frage 6 zur Kettenregel
Ihre beim Vortrag auf der BINNOTEC 2002
und im NET-Journal-Artikel
http://www2.mathematik.tu-darmstadt.de/~bruhn/NJ-Orig.doc
verwendete "Kettenregel" haben Sie, offenbar unter dem Druck von Beanstandungen, in Ihrem kürzlich erschienenen Buch EMV-3 durch die Regel (27.11)
(K) dV(r(t))/dt = dr(t)/dt · grad V |r=r(t)
ersetzt, wenn man die (sehr ungebräuchliche) Schreibweise ∂V(r=r(t))/∂r als grad V|r=r(t) interpretiert. Aber die Felder der Elektrodynamik sind nicht nur ortsabhängig wie V = V(x), sondern auch zeitabhängig: E = E(x,t).
Die Wellen der Elektrodynamik hängen häufig
von der Kombination t−e·x/c mit einem konstanten Einheitsvektor e ab,
z.B.
E(x,t) = E0 eiω(t−e·x/c)
Fragen:
a) Halten Sie (K) bzw. (27.11) für anwendbar auf E(x,t) = E0 eiω(t−e·x/c)?
b) Wenn ja: Was ergibt sich für r(t) = r0 + vt und
dr(t)/dt
= v nach Ihrer Regel (27.11)?
c) Wenn nein, was nun?
Frage 7 zu Ihren Maxwell-Gleichungen
Von den Gleichungen (27.12-13) gibt es auf den Seiten 116 und 118 Ihres Buches EMV-3 zwei unterschiedliche Versionen, die nur übereinstimmen, wenn man u.a.
(M*) dE(t)/dt = ∂E/∂t
annimmt. Analoge Gleichungen verwenden Sie
auch sonst noch mehrfach, z.B. erkennt man dies beim Vergleich Ihrer
Fundamentalen Feldgleichungen (27.26) auf S. 118 und (27.26*) auf S. 122.
Fragen:
a) Glauben Sie an (M*)?
b) Wer hat das bewiesen?
Frage 8 zu einer Regel Ihrer neuen Vektorrechnung
Bei der "Herleitung" der Gleichung (27.27) aus (27.26*), auch schon in Ihrem
nachlesbar, machen Sie Gebrauch von der bisher völlig unbekannten Vektorregel
(M**) v·v g = v v·g.
für g = grad div B.
Fragen über Fragen:
a) Wem kommt die Ehre zu, die wichtige Gleichung (M**) bewiesen zu haben?
b) Was halten
Sie von dem Gegenbeispiel B = (0,y2,0) und v = (c,0,0)?
Das ergibt div B =
2y, g = grad div B =
(0,2,0),
daher v·v grad div B
= (0,2c2,0) ≠0,
aber v v · grad div B = v 0 = 0.
Frage 9 zur Neutralitätsbedingung in Luft oder Vakuum
Sie haben eine gewisse - in Hinblick auf die Konsequenzen
durchaus verständliche - Abneigung gegen die experimentell bestens gesicherte
Bedingung der Ladungsfreiheit in elektrisch neutralen Medien. Man weiß, dass
als Konsequenz des Coulomb-Gesetzes in jedem Medium das sogenannte
Flussintegral ∫Ω D · n do die im Innern einer beliebigen
geschlossenen Kontrollfläche Ω
vorhandene elektrische Ladung anzeigt. Daraus ergibt sich für Vakuum oder
normale Luft mathematisch die Maxwellsche Gleichung
div E = 0.
Fragen:
a) Welche
gegenteiligen experimentellen Befunde sind Ihnen bekannt?
b) Wissen Sie, dass Ihre "Skalarwellenbedingung" rot E = 0 aus
http://www.k-meyl.de/Aufsatze/Skalarwellen/Bild2.gif
zusammen mit der Neutralitätsbedingung div E = 0 sowohl die E-Wellengleichung
wie auch Ihre Fundamentale Feldgleichung (Version aus EMV-1, S. 76 (15))
trivialisieren?
Unter diesen Bedingungen sind keine Wellen, also erst recht keine Skalarwellen mehr möglich.
Frage 10 zu Ihrer neuen Fundamentalen Feldgleichung
Wissen Sie, dass auch Ihre neue Fundamentale Feldgleichung (Version aus EMV-3, S. 118) selbst unter
Verzicht auf die Maxwellsche Neutralitätsbedingung keine Skalarwellen-Anteile
bei ebenen Wellen zulässt? S. dazu
http://www2.mathematik.tu-darmstadt.de/~bruhn/NFFG.doc
Frage 11 zu M. Faradays Widerlegung "hydrotischer Terme" im Induktionsgesetz
Sie haben das Induktionsgesetz um einen "hydrotischen Term" H/τ2 zu
(M 27.20) rot E = − μ (∂H/∂t − H/τ2)
(s. (27.20) in EMV-3) erweitert.
Frage a) Ist Ihnen bekannt, dass M. Faraday bereits vor 1830 nachgewiesen hat, dass der Anteil b = H/τ2 (in Luft) stets Null sein muss?
|
M. Faraday hat lange Zeit, wie wir heute sagen würden, nach zirkulären elektrischen Spannungen, also nach rot E ≠ 0, in statischen Magnetfeldern (H ≠ 0 und ∂H/∂t = 0) gesucht, aber vergebens, mithin nach (M 27.20) die Gleichung 0 = − μ (0 − H/τ2) erwiesen oder wegen H ≠ 0 auch 1/τ2 = 0. Frage b) Welche experimentellen Befunde gibt es heutzutage, die für 1/τ2≠0 in Luft oder Vakuum sprechen? |
|
Frage 12 zur Begründung Ihrer Objektivitätstheorie
In Ihrem Buch EMV-3, S. 128, geben Sie als Quelle Ihrer Transformationsgleichungen das Buch von K. Simonyi, Theoretische Elektrotechnik 1979, S. 924 an. Dort aber findet man nur die Transformationsgleichungen
E' = E + v ×B und H' = H − v ×D.
Frage: Warum weichen
Ihre Transformationsgleichungen
E = v ×B und H = − v ×D
trotz des
Zitates von den Simonyi-Gleichungen ab?
Literatur
[1] K. Meyl: Potentialwirbel Band 1, 1990
[2] K. Meyl: Elektromagnetische Umweltverträglichkeit Teil 1, 2. Auflage 1997
[3] K. Meyl: Elektromagnetische Umweltverträglichkeit Teil 3, 2003
[4] G. W. Bruhn: Meyls Skalarwellen auf der BINNOTEC 2002
auf http://www2.mathematik.tu-darmstadt.de/~bruhn/
[5] G. W. Bruhn: Meyls Fundamentale Feldgleichung