The Normalform of a Space Curve and its Application to Surface Design

Erich Hartmann

Abstract:
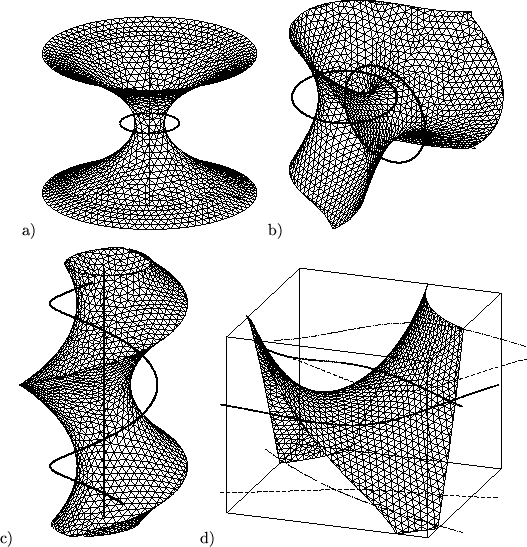
The normalform of a space curve is introduced analogously to the normalform of a plane curve and a surface. Its normalform function is (in difference to the latter cases) not differentiable in curve points. Despite of this disadvantage the normalform is a suitable tool for designing surfaces which can be treated as common implicit surfaces. Many examples show applications of the normalform to surface design.

Figure 1: Bisector surfaces between two lines/circles/curves
\begin{figure} \centerline{a)\epsfxsize=5cm \epsffile{vorcckg1.eps} b)\epsfxsiz... ... \epsffile{vorcchelix1.eps} d)\epsfxsize=7cm \epsffile{vorcc2.eps}}\end{figure}