Einführung in die mathematische Modellierung
Übungsstunde vom 26.5.2004
Prof. Dr. Martin Kiehl
Kachelmuster
Aufgabenstellung:
Es soll nach der Produktion von Kacheln, welche mit einem zufälligen Muster bedruckt sind, diejenigen aussortiert werden, welche eine zu gewaltige Abweichung aufweisen. Dazu werden die Kacheln einzeln abfotografiert. Die Aufgabe besteht nun darin, eine geeignete Metrik oder einen geeigneten Algorithmus zu finden, mit dem bei jedem beliebigen Zufallsmuster eine zu große Verschiedenheit erkannt wird, und so die Kachel ausrangiert werden kann.
1. Idee zur Lösung:
Eine erste spontane Lösungsidee war,
das Foto der Kachel in kleinere Felder aufzuteilen und danach die
"Durchschnittsfarbe" der jeweiligen Areale miteinander zu vergleichen. Als
Verbesserung ließe sich noch das Raster verkleinern, indem man die kleineren
Felder wiederum in Kleinere teilt usw.
Dieser Algorithmus überprüft, ob die mittlere Farbdichte mit dem Soll übereinstimmt.
Die Aufgabe ist allerdings durch diesen Ansatz zu wenig universell gelöst. Bei Kacheln, mit gleichmäßigem Muster, wie zum Beispiel Sprenkeln oder zufällig angeordneten Streifen (siehe Bodenbelag im alten Hauptgebäude) wird dieser Algorithmus funktionieren, allerdings werden bei Mustern mit Kacheln, die signifikant vom Mittel abweichen (z.B. Kacheln mit geometrischen Objekten), voraussichtlich zu viele aussortiert.
Die mit unserem Lösungsansatz gegebene Metrik verleiht Kacheln mit gleichem oder sehr ähnlichem Muster den Abstand 0 und sortiert andere aus, obwohl auch bei größeren Abständen die Kacheln optische zusammen passen könnten.
Das Fazit zum ersten Lösungsansatz lautet also, daß dieser Algorithmus die gleichmäßigsten zufällig gestreuten Kacheln auswählen wird, allerdings bei gröberen Mustern, wie zum Beispiel zufällig platzierte geometrische Objekte, nicht funktioniert.
2. Idee zur Lösung:
In diesem 2. Ansatz befassten wir uns ausschließlich mit dem Problem der geometrischen Objekte.
Die Idee war, verschiedene Restriktionen vom Kunden her zu erfassen, und die Kacheln dementsprechend zu sortieren. Anhand von Eigenschaften der Kacheln, wie
Hintergrundfarbe
Anzahl der Objekte
Art der Objekte
Abstand der Objekte
sollte nun eine Art Rahmen geschaffen werden, in welchem sich die Abweichungen befinden dürfen..
Um die Lösung noch weiter zu verallgemeinern betrachten wir nun nur noch eine Art von Objekten, die sich weder in Farbe noch Größe voneinander unterscheiden. Betrachtet werden soll der Abstand der Gebilde auf einer einzelnen Kachel.
Von vorneherein sollen solche Kacheln ausgeschlossen werden, deren Objekte sich überlappen oder den Rand der Kachel übertreten.
Nachdem die Kacheln vom Computer
erfasst wurden, und dieser durch entsprechende Software die Objekte als solche
erkannt und bestimmt hat, werden nun Radien um die Mittelpunkte erstellt, die
mit diversen Restriktionen belegt sind. Es könnte zum Beispiel ein Bereich
geben, d.h. eine Zone mit einem gewissen Abstand vom Objektmittelpunkt, in dem
sich kein weiteres Objekt befinden darf. An diese Zone grenzt eventuell eine
weitere an in der sich ein oder zwei Objekte aufhalten dürfen, usw. Diese Zonen
ließen sich noch gewichten, zum Beispiel könnte man bei einer Anzahl von 400
Kacheln festlegen, daß nur bei 40 Kacheln zwei Objekte dicht beieinander liegen
dürfen.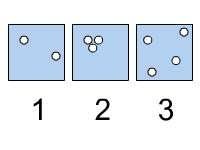 In
dem Beispiel würde die Kachel Nummer 2 aussortiert, da hier die Objekte, in
diesem Fall Kreise, zu dicht beieinander lägen. Allerdings könnte man auch
erwägen die erste Kachel auszusortieren, da sich hier nur 2 Objekte befinden.
In
dem Beispiel würde die Kachel Nummer 2 aussortiert, da hier die Objekte, in
diesem Fall Kreise, zu dicht beieinander lägen. Allerdings könnte man auch
erwägen die erste Kachel auszusortieren, da sich hier nur 2 Objekte befinden.
Mit der Erkennung der Farbe und der Art der Objekte kann dann dementsprechend umgegangen werden.
Das Fazit des zweiten Lösungsansatzes ist, daß durch eine Festlegung diverser Randbedingungen das Problem ein wenig universeller als im ersten Ansatz gelöst werden kann. Trotzdem ist dieser Entwurf noch nicht optimal. Es ist sehr viel Vorarbeit nötig, um die Randbedingungen des Algorithmus festzulegen. Außerdem kann es sein das nach Durchlauf aller Kacheln keine Einzige als in Ordnung eingestuft wird.
Stefan Kurowski