Der Fachbereich Mathematik der TUD veranstaltet in Zusammenarbeit mit dem Zentrum für Mathematik regelmäßig Schülermodellierungswochen. Das folgende Problem wurde während der Modellierungswochen 30. September - 5. Oktober 2001 in Höchst bearbeitet.

Katalysatoroptimierung

(© Fachbereich Mathematik der TU Darmstadt)

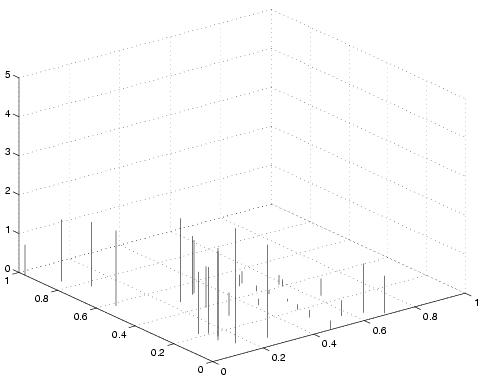
Bei der Katalysatorentwicklung werden unter anderem verschiedene Stoffgemische getestet und nach verschiedenen Kriterien wie Ausbeute, Wirkungsselektivität und Lebensdauer untersucht und bewertet. Im vorliegenden Fall soll eine optimale Legierung eines Trägermetalls mit zwei weiteren Metallen gefunden werden. Einige Legierungen sind bereits getestet, die Ergebnisse liegen vor. Da die Herstellung und Prüfung einer neuen Legierung sehr aufwendig ist und über eine Woche dauert, ist eine Strategie gesucht, nach der aussichtsreiche Testlegierungen vorgeschlagen werden können. Dabei ist zu beachten, daß in gleicher Zeit und nahezu zum gleichen Preis parallel gleich mehrere Legierungen hergestellt und getestet werden können.

Einige bewertete Katalysatoren mit verschiedenen Mischungsverhältnissen

Komponente 1 Komponente 2 Gütewert
0.47690214 0.48140207 0.28649985
0.14179896 0.20687931 1.70524819
0.14912877 0.16719984 2.18964970
0.49727283 0.49657351 0.30487407
0.41952603 0.31053632 0.16166484
0.56815714 0.07687569 0.39701165
0.58270102 0.41675064 0.24565671
0.68986715 0.01252851 0.96418020
0.50698814 0.37065679 0.09640155
0.49213196 0.20336682 0.13766550
0.64128453 0.05762833 1.26088010
0.05750571 0.85512684 1.58583413
0.47290604 0.00726387 0.20525623
0.11549088 0.22297126 1.59178954
0.26635363 0.06463858 2.38245898
0.15560684 0.08660494 2.94850378
0.28932907 0.29295558 0.59085829
0.32308939 0.51800141 1.36777362
0.27702141 0.39550776 1.05300917
0.10678562 0.76415570 1.64706034
0.58190954 0.39635089 0.18153609
0.12964932 0.14186196 2.36621630
0.24303682 0.48305780 2.14872155
0.00201311 0.97087245 0.77063582
0.51366720 0.28184586 0.06522857
0.31238239 0.51207353 1.50274272
0.62659484 0.25738802 0.44468115
0.48016947 0.12629727 0.18925600
0.06056585 0.57764297 1.93729467
0.49092422 0.41284775 0.14690791


Die Daten können angefordert werden, es lassen sich aber ganz einfach ähnliche Daten generieren. Man definiere sich eine Funktion mit vielen lokalen Maxima. Z.B. kann man mit unterschiedlichem Gewicht mehrere zweidimensionale Normalverteilungen mit zufälligen Mittelwerten $M_x$ und $m_y$ und zufälliger Varianz addieren

$f(x,y)=\sum_{i=1}^n w_ie^{\frac{(x-m_{xi})^2+(y-m_{yi})^2}{\sigma_i^2}}$.