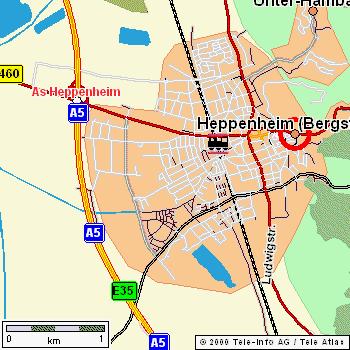
Die Stadt Heppenheim plant, rechtzeitig zum Hessentag 2004, eine Behelfsauffahrt von der L3398 auf die A5 südlich von Heppenheim. Dabei sollen die Ausfahrts- und Auffahrtsschleifen optimal ausgelegt werden!

Die Befürworter rechnen mit Baukosten von etwa 19 Millionen DM.
Meterpreise einer 3 Meter breiten Straße: DM 900.-
Ackerlandquadratmeterpreise im Bereich der Kreuzung A5/L3398: DM 10.-
Verkehrszählung an den Knotenpunkten A5/B460 sowie B460/Tiergartenstraße/Am Entenpfad:
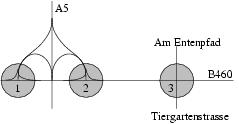
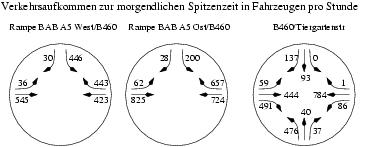
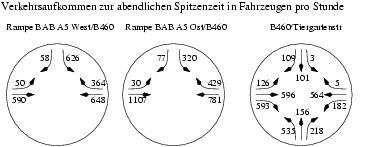
Die Tagesgesamtbelastung entspricht etwa dem zehnfachen der Stundenspitze.
Maximale Querbeschleunigung im Scheitelpunkt einer Kurve (Beziehung Geschwindigkeit zu Krümmungsradius):
| Geschwindigkeit in km/h | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| Krümmungsradius in m | 45 | 80 | 120 | 180 | 250 | 340 | 450 |
Es ist üblich in den Abbiegespuren mindestens 40 km/h zu ermöglichen.
Stetigkeitsanforderung:
Das Lenkrad muß stetig bewegbar sein (global $C^2$-stetig).
Maximale Änderung des Krümmungsradius: 0.5 $[m/s^3]$.
Stückweise ist jedoch $C^3$ verlangt.
Minimale Länge eines $C^3$-Teilstückes: 2 Sekunden Fahrzeit.
Der sprunghafte übergang von einem Kurvenstück mit konstanter Lenkbewegung
in einen anderen (Gerade-Klotoide, Klotoide-Kreis)
muß optisch erkennbar sein.
Daher müssen die Teilstücke wenigstens 2 Sekunden dauern.
Maximale Bremsverzögerung, die Autofahrern
in einer Autobahnausfahrt zugemutet werden darf:
Ausfädelstreifen sind mit 250 m vorgegeben.
Dabei erfolgt die Verzögerung auf die Geschwindigkeit mit der die Kurve gefahren werden soll.
In der Kurve soll weder gebremst noch beschleunigt wereden.
Entsprechend umgekehrt bei Beschleunigungsstreifen.
Bei Ampeln soll ausreichend Stauraum zur Verfügung stehen,
der auch in Spitzenzeiten in der Regel genug Platz zum Bremsen läßt
(bei 40 km/h etwa 15 m).
Durchschnittsgeschwindigkeiten auf der rechten Spur der A5: 100 km/h.
Durchschnittsgeschwindigkeiten auf der L3398: 60 km/h.
Winkel zwischen A5(süd) und L3398(west): Aus Karte ablesbar ca. 50 Grad
Zwischen den Schenkeln A5(süd) und L3398(ost): Flugplatz, daher kein Platz für eine Ausfahrt.
An der A5 Richtung Süden Parkplatz gleich nach der Kreuzung.
Er kann aber überbaut werden.
Die Aufgabe eignet sich für verschiedene Jahrgangsstufen.
Schulerfahrungen:
Kursleiter: Martin Kiehl
Klassenstufe: 13. Klasse
Auswahl der Schüler Preisträger beim Tag der Mathematik
Bearbeitungszeit: 1 Woche
Kontakt: kiehl at mathematik. tu-darmstadt. de
Kursleiter: Hans Krauss
Klassenstufe: 8. Klasse des gymnasialen Zweiges (Altkönigschule, Kronberg/Ts)
Auswahl der Schüler: normaler Klassenverband
Bearbeitungszeit: 6 Stunden innerhalb von 2 Wochen
Kontakt: hanskrauss at aol. com
Literatur: Martin Kiehl: Eine Autobahnauffahrt planen - Mathematische Modellierung mit Schüern, in Friedrich Jahresheft XXI Aufgaben, Lernen fördern - Selbständigkeit entwickeln, 2003 p.121-125.
Weitere Lösungswege auf Anfrage.
Kontakt: kiehl at mathematik. tu-darmstadt. de