Zur DGEIM-Tagung an der Universität Stuttgart

am 25. Oktober 2003

von Gerhard W. Bruhn, Technische Universität Darmstadt

Übersicht K. Meyl hat seine Skalarwellen als Vektor-Lösungen seiner Fundamentalen Feldgleichung (FFG) definiert, die ein skalares Potential besitzen (Skalarwellenbedingung (S)). Naturgemäß bewegen sich Wellen von der Stelle, und das hat Meyl auch verschiedentlich in Abbildungen dokumentiert. Er hat jedoch übersehen, dass man die allgemeine Lösung von (FFG) und (S) leicht bestimmen kann. Es zeigt sich, dass alle möglichen Lösungen ortsfest sind. Bewegliche, d.h. Meylsche Skalarwellen, kann es nicht geben.

Die DGEIM (www.dgeim.de) ist vom UNI-KURIER in ihrem Gründungsjahr 1999 vorgestellt worden; danach nie wieder, obgleich doch Tagungen dieser Gesellschaft an der Universität Stuttgart unter Schirmherrschaft von Prof. Dr. Ing. B. Kröplin auch in den Jahren 2000 und 2002 stattfanden. Über die Gründe mag man mutmaßen, einiges davon wird klar, wenn man den Bericht in Unikurier Nr. 82/83 (September 1999) genau liest, wo von "bioenergetischen Meßmethoden zur medizinischen Diagnose und Therapie" die Rede ist.

Am 25.Oktober 2003 veranstaltet die DGEIM auch ihr 5. Symposium auf dem Campus der Universität Stuttgart, Schirmherr ist wie in den Vorjahren Prof. Dr. Ing. B. Kröplin. Das Tagungsthema lautet

"Gibt es eine Skalarwellenmedizin?"

Was sind Skalarwellen? Skalarwellen sind hypothetische elektrische Wellen einer besonderen Art, die von dem stellv. DGEIM-Vorsitzenden Prof. Dr. Ing. K. Meyl, FH Furtwangen, erfunden wurden. Diese Skalarwellen waren in der letzten Zeit u.a. ein heiß diskutiertes Thema im alternativ-medizinischen Bereich. Z.B. gab es in den Heften 12/2002, 01-04/2003 der Zeitschrift CO’MED (= Complementär-Medizin) Beiträge und langwierige Diskussionen zum Thema "Skalarwellen". Auf dem DGEIM-Symposium soll nun die Frage nach einer "Skalarwellenmedizin" beantwortet werden, wobei aus dem Vortragsprogramm hervorgeht, dass die Veranstalter für die "Skalarwellenmedizin" die Antwort "JA" anstreben, um diesen Bereich wissenschaftlich zu untermauern.

Wir wollen die Leser hier an ein paar einfache ingenieurwissenschaftliche Tatsachen erinnern, welche eher die Antwort "NEIN", denn ein "JA" begründen.

s. auch http://www2.mathematik.tu-darmstadt.de/~bruhn/Skalarwellen-einfach.htm

K. Meyl hat aus erweiterten Maxwell-Gleichungen für das elektrische Feld eine von ihm als "Fundamentale Feldgleichung" bezeichnete Gleichung hergeleitet ( [3], S.118):

(FFG) − c² rot rot E − E_tt = (α + β) E_t + αβ E,

die eine Variante der gedämpften Wellengleichung

c²ΔE − E_tt = (α + β) E_t + αβ E

darstellt. Die Koeffizienten α,β sind hierbei positive Konstanten und c ist die Lichtgeschwindigkeit.

Skalarwellen sind nach Meyl Wellen-Lösungen seiner FFG, bei denen der Lösungsvektor E ein skalares Potential besitzt. Dafür gibt es die bekannte Bedingung

(S) rot E = 0.

Der Rest ist einfach: Einsetzen der Bedingung (S) in (FFG) ergibt (unter leichter Umstellung)

E_tt + (α+β) E_t + αβ E = 0.

Das ist an jeder festen Stelle x eine gewöhnliche Differentialgleichung 2. Ordnung mit konstanten Koeffizienten, die dem Leser vielleicht in der Form

E^·· + (α+β) E^· + αβ E = 0.

vertrauter ist. Die Lösung kann in jeder Formelsammlung (z.B. im "Bronstein") nachgeschlagen werden: Die allgemeine Lösung lautet

(MW.a) E(x,t) = E₁(x) e^−αt + E₂(x) e^−βt für α ≠ β

und

(MW.b) E(x,t) = [E₁(x) + t E₂(x)] e^−αt für α = β,

wobei die Koeffizientenvektoren E₁(x) und E₂(x) willkürlich vorgegeben werden dürfen. Zur Erfüllung der Bedingung (S) hat man in (MW.a,b) noch E_k = grad U_k mit willkürlichen Potentialfunktionen U_k zu setzen. Wir wollen diese Lösungen (MW.a,b) nach ihrem Entdecker "Meyl-Wellen" nennen.

Man kann sofort sehen, dass die "Meyl-Welle" ortsfest ist, also einen einmal eingenommenen Bereich nie verlässt. Denn wählt man z.B. die Potentialfunktionen

U₁(x) und U₂(x) ≡ 0 außerhalb einer Kugel,

so bleibt die "Meyl-Welle" für alle Zeiten im Innern der Kugel, ist also ortsfest: Die "Meyl-Welle" bewegt sich nicht und hat damit die Bezeichnung "Welle" nicht verdient. Man vergleiche dies mit der Meylschen Vorstellung von Skalarwellen in [3], S.20-22, wo die Skalarwelle sich mit einer Geschwindigkeit v≠0 fortbewegt:

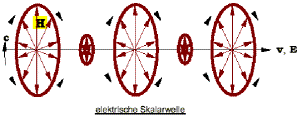
Somit haben wir das Ergebnis:

Weil die "Meyl-Wellen" keine echten Wellen sind, gibt es keine Skalarwellen.

Die Antwort auf die Titel-Frage der DGEIM-Tagung lautet damit "NEIN". D.h. man kann die Tagung auch absagen, da man ja schlecht einen Tag lang über nichts anderes als NICHTS reden kann.

Ein Beispiel

Wir untersuchen einen "Skalarwellen-Sender" innerhalb einer Kugel |x| < R und seine Wirkung auf den Außenraum |x| ≥ R.

Die Meylwelle (MW.a) besitzt das Potential

(U.a) U(x,t) = U₁(x) e^−αt + U₂(x) e^−βt für α ≠ β.

Man kann U(x,t) unmittelbar als Verlauf der elektrischen Spannung zur Zeit t deuten.

Betrachten wir unter der Annahme α > 0 den ersten Summanden für sich. Es sei der Anfangsverlauf U₀(x) der Spannung in der Sender-Kugel |x| < R gegeben. Im Außenraum herrsche anfangs (für t=0) Feldfreiheit mit Spannung Null, d.h. U₀(x) ≡ 0 für |x| ≥ R. Dann ergibt sich der weitere Spannungsverlauf für t > 0 zu

U(x,t) = U₀(x) e^−αt innerhalb der Kugel,

während außerhalb der Kugel wegen U₀(x) ≡ 0 weiterhin

U(x,t) = 0 · e^−αt ≡ 0 und E(x,t) = grad U ≡ 0

gilt, die Spannung und somit auch das elektrische Feld im Ruhezustand verbleibt:

Ergebnis:

Die "Meyl-Welle" verlässt die Sender-Kugel nicht. Der Außenraum bleibt feldfrei.
Die "Meyl-Welle" klingt im Innern der Sender-Kugel exponentiell ab.

Analog kann man auch mit dem zweiten Summanden der Gleichung (U.a) verfahren. Für die Kombination (U.a) selbst hat man zu bedenken, dass als Anfangsbedingung außer dem Spannungsverlauf noch die anfängliche Spannungsänderung U_t(x,0) (infolge für t = 0 fließender Ströme) vorgegeben werden muss. Das ergibt dann außerhalb der Sender-Kugel die Bedingungen U(x,0) ≡ 0 und U_t(x,0) ≡ 0 mit der Konsequenz

U₁(x) ≡ U₂(x) ≡ 0

und damit auch

U(x,t) ≡ 0 und E(x,t) ≡ grad U ≡ 0 im Außenraum,

d.h. wiederum Feldfreiheit im Außenraum |x| > R für alle t > 0.