Meyl (kursiv)
diskutiert mit Bruhn (Normalschrift)
M: Ich habe unmißverständlich aber sachlich die von Bruhn verbreitete Unwahrheit richtig gestellt: Ich arbeite mit der Maxwell-Theorie, ich leite sie sogar her, weshalb sie bei mir ohne Einschränkung weiter Gültigkeit besitzt.
B: Die Herleitung ist aus mehreren Gründen falsch. Zunächst sind Meyls "Grundgleichungen" (27.3-4) in EMV 3 oder
http://mitglied.lycos.de/hartiberlin3/day3/binnotec_day3_031.jpg (Link ist veraltet)
falsch, weil nicht allgemeingültig. Schon die aus zwei gegenläufigen periodischen ebenen Wellen resultierende stehende Welle genügt diesen "Grundgleichungen" nicht mehr. Das kann unter Frage 2 in
http://www2.mathematik.tu-darmstadt.de/~bruhn/Zwoelf-Fragen.htm
nachgelesen werden. Es kann später noch ausführlich diskutiert werden.
Überdies sind diese Grundgleichungen nur für |v| = c (nichttrivial) lösbar, wie Meyl selbst auf S.126 (28.5) von EMV 3 feststellt. Damit sind seine Spekulationen über die Fälle |v| < c und |v| > c z.B. in seinen Vorträgen obsolet. Für |v| ≠ c gibt es keine Lösungen E ≠ 0. Daran kann auch der Lösungsversuch mit einer "Potenzreihe" auf S.128 nichts ändern. Das geht eben nur für E0 = 0, d.h. E = 0.
Weiteres unten bei Besprechung der Regel (M).
Überdies gehört
zur Maxwell-Theorie in elektrisch neutralen Medien wie Luft oder Vakuum
die Maxwell-Bedingung div E = 0
(Ladungsdichte = 0) (vgl. z.B. F.A. Popp’s DGEIM-Vortrag). Dann steht das
"Skalar" div E nicht zur Erzeugung von
Skalarwellen zur Verfügung, da immer Null: Skalarwellen sind Null-Wellen. Das folgt aus der Maxwell-Theorie.
M: Bruhn ... verfasst neue
Traktätchen im Internet und schreibt neben allerhand Polemik: laut Prof. Meyl
handle es sich bei rot E =0 um die Skalarwellenbedingung! Da hat sich der Herr
Bruhn aber etwas aus den Fingern gesaugt und diesen, seinen Fehler dann mir in
die Schuhe geschoben! In meinen Skripten steht nichts derartiges.
B: Was wäre dann das? Das steht bei K. Meyl: EMV 3, S.9. Gleiches findet man auch auf S.6 und S.8:

oder das?

Quelle: Bild 2 in http://www.k-meyl.de/go/60_Primaerliteratur/Scalar-Waves.pdf
Bemerkung: Die Maxwell-Gleichung div E = 0 für neutrale Medien reduziert die 2. Gleichung (21.4) auf ∂2E/∂t2 = 0, und mit (21.6) reduziert sich (21.7) auf ∂2φ/∂t2 = 0. Beides lässt gar keine Wellen mehr zu - wenn man wirklich Maxwell-Theorie betreibt.
M: Richtig ist doch vielmehr, dass rot E =0 die Bedingung dafür ist, dass die von der
Maxwelltheorie beschriebenen Transversalwellen zu Null werden, so wie umgekehrt
div E =0 die Skalarwellen zu Null setzt.
B: Gewiss, eine Welle hat allgemein eine Transversal- und eine Longitudinalkomponente. Was bei rot E = 0 dann noch übrig bleibt, sind die Longitudinalwellen (von Meyl auch Skalarwellen genannt). Also ist (21.4), wie in Meyls Texten (s.o.) festgestellt, die Bedingung für Skalarwellen. Da kann man doch nicht nachträglich hergehen, und die einmal gestellte Bedingung rot E = 0 einfach wieder vergessen. In beiden gezeigten Bildern steht, insgesamt dreimal in EMV 3 unter (21.4):
Skalarwellen (oder Longitudinalwellen) genügen den Gleichungen
rot E = 0 und grad div
E = 1/c2 ∂2E/∂t2 (21.4)
Auch das Wörtchen "und" steht da dreimal! Das heißt doch wohl: Nicht ohne rot E = 0.
M: Dies ist sicher unstrittig. Die von Bruhn vorgenommene Umkehrung ist mathematisch
unzulässig. Wieso fällt das Bruhn nicht auf, der vorgibt, Mathematiker zu sein?
Wenn ich die Wellengleichung anschreibe, wie in meinem Vortrag, dann treten
dort immer beide Terme auf. Sie sind also nicht Null, wie es Bruhn
unterstellt.
B: Das hat Bruhn nicht unterstellt, das hat Meyl dreimal geschrieben. Auch wenn man einen Term hinschreibt, ist der deswegen nicht schon automatisch ungleich Null. Das kommt darauf an, was man über diesen Term (rot E) vorher gesagt hat (oder noch sagen wird). Und Meyl hat dem Leser 3 × (21.4) mitgeteilt.
M: Der neueste Angriff trägt die gleiche hinterlistige Handschrift.
B: Na na, schön friedlich bleiben, bitte!
M: Ausgangspunkt ist die Anwendung der Kettenregel (K.Meyl: EMUV Teil 3, Gleichung 27.11) z.B. auf die Induktion B(x(t)). Meine Rechnung ist geprüft worden und in keiner Weise zu beanstanden.
B: Doch, Herr Meyl, man kann! Wer war denn Ihr Prüfer? Es liegt eine simple Verwechslung
von B(x(t)) mit dem in der
Elektrodynamik auftretenden B(x,t) vor. Der Unterschied hat allerdings schwerwiegende Folgen:
Betrachten wir
das Beispiel einer ebenen B-Welle,
die sich in Richtung k (|k| = 1) mit der Geschwindigkeit v = ck durch den Raum bewegt,
z.B.
B = B0 sin (k·x −
ct).
Dann ist B eine durch die rechte Seite
gegebene Funktion von Ort x und Zeit t. Dafür schreibt man B = B(x,t) (und nicht
B(x(t)) wie Meyl). Unzweifelhaft sind alle
raumzeitlich veränderlichen Felder von Ort x und Zeit t abhängig, also z.B. E
= E(x,t), H = H(x,t) usw.
Man kann Ort x und Zeit t unabhängig voneinander vorgeben und dann das Feld nach der Formel
berechnen. Das ist die Situation, wie man sie in der Elektrodynamik überall antrifft.
Was aber wäre mit Meyls B(x(t)) gemeint? Die Klammern geben die Reihenfolge der Berechnung vor: Zunächst muss bei bekanntem t die Größe x(t), also eine von t abhängige Stelle, berechnet werden. Mit x(t) beschreibt man Bahnkurven im Raum, z.B. eine Schraubenbewegung mit der konstanten Kreisfrequenz ω = 2π/T um den Nullpunkt im Abstand R mit Ganghöhe H durch
x(t) = (R cos ωt, R sin ωt, H/T t)
(Stichwörter im "Bronstein": Schraubenlinie, Parameterdarstellung einer
Raumkurve u.ä.).
In einem zeitlich konstanten Feld B(x)
meint man mit B(x(t)) den Feldvektor an der zuvor berechneten Stelle x(t).
Meint Herr Meyl das auch? Wenn ja, erhält er mit B(x(t)) nur den Feldvektor längs der einen Raumkurve x = x(t).
Was kann man damit in der Elektrodynamik anfangen, da man es mit
raumzeitlich veränderlichen Feldern zu tun hat? Und welche Bahnkurve meint Herr
Meyl denn?
Wäre eine Raumkurve gegeben, die gemäß x = x(t) zeitlich durchlaufen wird, dann hätte es Sinn, nach der zeitlichen Änderung des Feldes B(x) längs der Bahn zu fragen. Dafür gibt es in der Tat etwas ähnliches wie Meyls Regel (M),
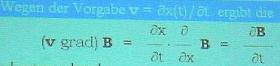
aus
http://mitglied.lycos.de/hartiberlin3/day3/binnotec_day3_033.jpg (Link veraltet)
nämlich die mehrdimensionale Kettenregel (K)
d/dt B(x(t)) = dx(t)/dt · [grad B(x)] |x=x(t)
aber diese Regel ist für den bei Meyl
vorliegenden Fall eines raumzeitlich veränderlichen Feldes elektrodynamischen
Feldes B(x,t)
nicht anwendbar, weil keine
Bahnkurven definiert sind und weil B nicht nur orts-, sondern auch zeitabhängig ist: B(x und t)
Meyl hat B(x,t) mit B(x(t)) verwechselt, und das ist nicht dasselbe,
wenn es auch so ähnlich aussieht.
Natürlich könnte man auch die Frage stellen, wie denn bei einem elektrodynamischen Feld B(x,t) die Zeitableitung längs einer gegebenen Bahn x = x(t) aussehen würde. Dazu müsste man die
Ableitung d/dt B(x(t),t) berechnen. Die Zeitabhängigkeit von B(x(t),t) käme durch die Bahnbewegung, aber
zusätzlich auch durch die Änderung von B an fester Stelle x zu Stande. Die Kettenregel weist für diesen Fall noch einen zusätzlichen
Summanden auf, der die Änderung von B an fester Stelle x wiedergibt (hier
rot gefärbt):
d/dt B(x(t),t) = dx(t)/dt · [grad B(x,t)] |x=x(t) + ∂B(x,t)/∂t |x =x(t)
Aber das ist für den vorliegenden Fall der
Elektrodynamik natürlich auch nicht verwendbar.
M: Herr Bruhn
aber geht her und gibt 2 Beispiele an, die gar nicht zutreffend sind.
B: Für den elektrodynamischen Fall B(x,t) schon. Ich dachte, um den geht es Herrn
Meyl.
M:
Einmal streicht er die Abhängigkeit von x und bei seinem zweiten Versuch setzt er die
Abhängigkeit von t zu Null. Abweichungen im Ergebnis sind zu erwarten, da Bruhn
von ganz anderen Voraussetzungen ausgeht.
B: Mit der Schreibweise
B(x,t) ist selbstverständlich
auch der Fall reiner Zeitabhängigkeit, also B(t), wie auch der Fall reiner Ortsabhängigkeit (Magneto-Statik)
eingeschlossen. Eine Regel wie Meyls Regel (M)
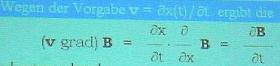
muss für jeden mit B(x,t) erfassbaren Fall gelten, sonst ist sie falsch.
M: Mit dem allgemeinen Fall, den ich berechne, befasst er sich erst gar nicht, will aber Glauben machen, Meyl hätte eine neue Regel in der Mathematik begründet, die Regel (M), die nach seinem Befinden falsch ist.
B: Das wollen wir mal überprüfen:
In
der abgebildeten Meyl-Regel kommen die Größen
v · grad B
links und ∂B/∂t
rechts vor. Wenn es für eine
behauptete Regel Gegenbeispiele gibt, so ist die Regel eben falsch, weil man ja
nicht wissen kann, welcher Fall bei einer späteren Anwendung gerade vorliegt, ein günstiger oder ein
ungünstiger Fall. Wir überprüfen ein paar Fälle unter Verwendung eines
gegebenen konstanten v ≠ 0:
|
Fall Nr. |
B(x,t) |
v · grad B |
∂B/∂t |
Bewertung |
|
1 |
v t |
0 |
v |
falsch |
|
2 |
x |
v |
0 |
falsch |
|
3 |
x + v t |
v |
v |
richtig |
|
4 |
x − v t |
v |
− v |
falsch |
Offenbar liefert von vier Fällen nur einer ein
richtiges Ergebnis. Man kann aber die Regel (M) zu einer richtigen machen, wenn
man die Anwendung auf Beispiele der Form B(x+vt) einschränkt. Für alle Fälle B, die nicht in
der Form B(x+vt) darstellbar sind, ist die Regel (M) falsch. Das bedeutet,
dass die Regel (M) ohne Benennung einer Einschränkung an B falsch ist; und Meyl hat keine Einschränkung
angegeben.
M: Was Bruhn
nicht sagt ist, dass es sich doch nur um seinen eigenen Fehler handelt. Und das
ist nicht seine erste bzw. zweite Unterstellung dieser Art!
B: Ach, Herr Meyl, wenn das doch so einfach wäre. Wenn man schon B(x,t) und B(x(t)) nicht unterscheiden kann, wären wohl etwas vorsichtigere Formulierungen angebracht.
Aber macht nichts, es war mir ein Vergnügen.
09.11.2003 Gerhard W. Bruhn