 |
Das Ziel der Darstellenden Geometrie ist, Bilder von räumlichen
Gegenständen wie Häuser, Maschinenteile ... in einer Zeichenebene
herzustellen. Dabei verwendet man hauptsächlich zwei Methoden:
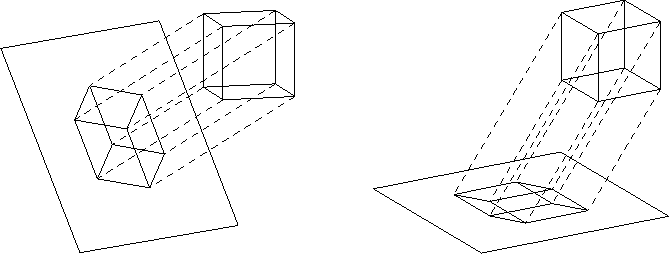
I) Parallelprojektion.
Hierbei projiziert man die Objekte (Punkte, Kanten, Kurven,...) mit
Hilfe paralleler Strahlen auf eine Ebene (Bildtafel). Steht die
Bildtafel senkrecht zu den Projektionsstrahlen, so spricht man von
senkrechter Parallelprojektion im anderen Fall von
schiefer Parallelprojektion. Projiziert man schief auf
eine horizontale Ebene (z.B. x-y-Ebene), so nennt man diese Art
Vogelperspektive. Bei einer Kavaliersperspektive
projiziert man schief auf eine senkrecht stehende Ebene.
II) Zentralprojektion.
Dem Sehen ähnlicher ist die Zentralprojektion. Hier werden die
Objekte mit Hilfe von durch einen Punkt Z (das Zentrum oder der
Augpunkt) gehende Strahlen zur Abbildung auf einer Bildtafel benutzt.
Die Gestaltungsmöglichkeiten bei Zentralprojektion ist durch die Verwendung der zusätzlichen Parameter Augpunkt und Distanz (des Augpunktes zur Bildtafel) vielfältiger. Arbeitet man mit Zirkel und Lineal, so ist allerdings der Aufwand zur Erstellung einer Zeichnung wesentlich größer. Auch bei Verwendung eines Rechners muß man den Vorteil von ''schönen'' Bildern durch eine etwas längere Rechenzeit erkaufen, da eine Zentralprojektion, im Gegensatz zu einer Parallelprojektion, nicht durch eine lineare Abbildung beschrieben werden kann. In der Technik gibt man i.a. der senkrechten Parallelprojektion den Vorzug, da bei Parallelprojektionen Proportionen (Teilverhältnisse) erhalten bleiben. Die meiste Zeit bei der Darstellung von Kurven und Flächen nehmen allerdigs sog. Hiddenline-Algorithmen in Anspruch. Sie sorgen dafür, dass verdeckte Kurven nicht gezeichnet werden.