TUD-Homepage von Erich
Hartmann:
Informationen zu
Lehre
&
Forschung
 , Adresse
/ address
,
, Adresse
/ address
, ,
, 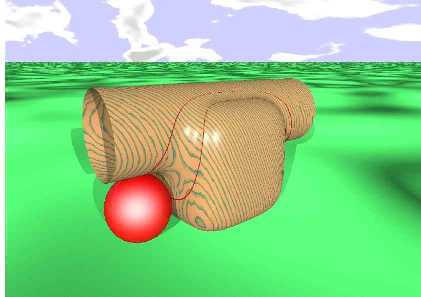
wertvolle Mathematik
Übergangsfläche
(blending surface)
A) Geometrische
CAD-Grundlagen
Skript/lecture
notes Geometry and Algorithms for CAD:
CAD-script
(WS 03/04),
nur Inhalt/contents only: Inhalt/contents
(Bei Problemen mit der pdf-Datei "CAD-script"
/ problems ? :
1) anclicken
2) "speichern als" / "save as"
3) BROWSER BEENDEN / EXIT BROWSER
4) die gespeicherte Version mit
"acroread" anschauen und eventuell drucken / display
and/or print file.)
Übungen: 1.Übung,
2.Übung,3.Übung,
4.Übung,
5.Übung,
6.Übung,
7.Übung,
8.Übung,
9.Übung,
10.Übung
altes
Skript
Computerunterstützte
Darstellende und Konstruktive Geometrie (1998, deutsch)
B) Software
zur
Darstellung von Kurven und Flächen / software
for displaying curves and surfaces:
(Hiddenline-Algorithmus,
Triangulierung von Flächen / hiddenline
algorithm, triangulation / polygonization of surfaces)
Das Programm-Paket
entält PASCAL-Programme / contains PASCAL source
codes for
a)
zum Zeichnen von Polygonzügen (parametrisierte Kurven) / displaying
polylines (parameterized curves)
b)
zum Berechnen von Polygonzügen auf impliziten Kurven
/ displaying implicit curves
c)
zu Aufgaben aus der Analytischen Geometrie / solving
problems of Analytical Geometry
d)
zu einem Hiddenline-Algorithmus für
nicht konvexe Polyeder (parametrisierte
Flächen) /
hiddenline-algorithm for non convex polyhedrons (parameterized surfaces)
e)
zur Triangulierung impliziter Flächen /
triangulation
of implicit surfaces (marching algorithm)
f)
zur Erstellung von Postscript-Dateien der angefertigten Zeichnungen.
/ generation of Postscript-files .
Die englische Version enthält
den "Cutting-Cubes"-Algorithmus von
M. Schmidt zum Polygonalisieren impliziter Flächen.
The english-version
contains the "cutting-cubes"-algorithm of M.Schmidt for polygonization
of implicit surfaces.
1) Beschreibung
(Probleme mit pdf-datei ? : siehe A) )
2) Programme
(mit " tar -xf ..." auspacken. )
2') source
code (engl. version, description:
see CAD-script above)
Hinweis: a) Falls bei der
Installation mit "make" etwas schief gegangen ist, kann mit "make cleanall"
der Urzustand wieder hergestellt werden !
b) Bei Verwendung neuerer FREE-PASCAL-Compiler muss "uses linux" durch
"uses Unix" ersetzt werden !
3) CAD mit PYTHON: PyCad
Raytracing Bilder von triangulierten
Flächen oder algebraischen Flächen lassen sich mit POVRAY
(s. Linux-Distr.) erzeugen.
Ein weiterer Raytracer für algebraische
Flächen findet man hier: surf-homepage
C) Mathematik f.
Bauingenieure / Mathematics
f.
civil engineers:
WS
00/01 , SS
01 , WS
02/03, SS
03,
WS
03/04, SS
04
D) Mathematik f.
Chemiker & Lehramt an Berufsschulen / Mathematics
f.
chemists & teachers f. vocational schools:
WS
01/02, SS
02 , WS
04/05 , SS
05, WS
05/06, SS
06
E) Darstellende Geometrie f.
Bauingenieure (WS
05/06) / Descriptive
Geometry f. civil engineers
Skript
(vollständig), Skript,
Seiten 1-4 (Inhaltsverz.)
Homepage
der Vorlesungim
WS 05/06 (link zu "Lehrmaterial") .
Homepage zur früheren Vorlesung WS
02/03
F) Darstellende Geometrie für
Architekten (SS05)
/ Descriptive Geometry
f.
architects
Skript,
Teil 1 (DG 1) , Skript,
Seiten 1-8 (Inhaltsangabe, Einleitung)
Skript, Teil 2 (DG 2)
(Homepage der Vorlesung
im SS 05 )
G) Projektive Geometrie / Projective
Geometry
Kurzskript
der Vorlesung im SS 2006
. Die Homepage zur Vorlesung
ist hier
zu finden.
Die meisten
Beweise von Aussagen über Kegelschnitte und Quadriken sind
im Skript
circlegeom
über Kreisgeometrien (s. H) ) enthalten.
H) Kreisgeometrien / Circle
Geometries
Unter
Kreisgeometrien versteht man eine Verallgemeinerung der Geometrien
der ebenen Schnitte auf
a) der Kugel ( Möbius-Ebene ), b) dem Zylinder
( Laguerre-Ebene ) und c) dem (einschaligen)
Hyperboloid ( Minkowski-Ebene ):
Deutsche Einleitung: Kreisgeom-Einl
English introduction (pages 1-9 of lecture notes below): circlegeom-introd
Circle
geometries are generalizations of the geometries of plane sections of
a) a sphere ( Moebius-plane ), b) a cylinder (
Laguerre-plane
)
and c) a hyperboloid of one sheet ( Minkowski-plane
)
Vollständiges
Skript (englisch) / lecture
notes: circlegeom
Das Skript enthält neben einem
Kapitel über grundlegende Aussagen über affine und projektive
Geometrie auch
ein ausführliches Kapitel über
Kegelschnitte
und ihre Charakterisierungen ( durch Symmetrien , Pascal-Theorem
und seine Ausartungen ,
Satz von Steiner , Satz von Qvist ,
Satz von Segre , ...)
The lecture notes
contain essential statements on affine and projective geometry. A second
chapter deals with important characterizations
of conics
( by symmetries , Pascal's Theorem , Steiner's Theorem , Qvist's Theorem
, Segre's Theorem,...)
I) Lust auf mehr
Geometrie / more Geometry ?
TU
Wien
J) Neuere Publikationen
/ recent papers
Publikationen
1975-2001 / papers 1975-2001
K) Wann ist Frühlingsfest
/
Chinese New Year ? 14.2.2010,
3.2.2011, 23.1.2012,
10.2.2013
Das chinesische Frühlingsfest
oder chinesische Neujahr ist das wichtigste chinesische Familienfest.
Es findet an keinem festen Tag
im Jahr statt. Eine Faustregel ist:
Frühlingsfest
ist am 2. Neumond (der Mond ist nicht zu sehen) nach Winteranfang (Peking-Zeit
!).
Die
genaue Regel ist hier zu finden.
xin nian hao !
Mehr
/ more:
National
Uni Singapore (NUS)
 , Adresse
/ address
,
, Adresse
/ address
, ,
, 